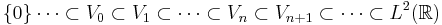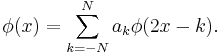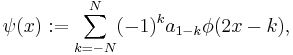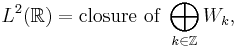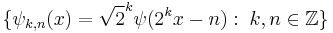Multiresolution analysis
A multiresolution analysis (MRA) or multiscale approximation (MSA) is the design method of most of the practically relevant discrete wavelet transforms (DWT) and the justification for the algorithm of the fast wavelet transform (FWT). It was introduced in this context in 1988/89 by Stephane Mallat and Yves Meyer and has predecessors in the microlocal analysis in the theory of differential equations (the ironing method) and the pyramid methods of image processing as introduced in 1981/83 by Peter J. Burt, Edward H. Adelson and James Crowley.
Contents |
Definition
A multiresolution analysis of the space 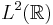 consists of a sequence of nested subspaces
consists of a sequence of nested subspaces
that satisfies certain self-similarity relations in time/space and scale/frequency, as well as completeness and regularity relations.
- Self-similarity in time demands that each subspace Vk is invariant under shifts by integer multiples of 2-k. That is, for each
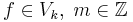 there is a
there is a 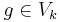 with
with 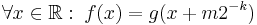 .
. - Self-similarity in scale demands that all subspaces
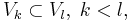 are time-scaled versions of each other, with scaling respectively dilation factor 2l-k. I.e., for each
are time-scaled versions of each other, with scaling respectively dilation factor 2l-k. I.e., for each 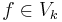 there is a
there is a 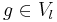 with
with 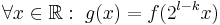 . If f has limited support, then as the support of g gets smaller, the resolution of the l-th subspace is higher than the resolution of the k-th subspace.
. If f has limited support, then as the support of g gets smaller, the resolution of the l-th subspace is higher than the resolution of the k-th subspace.
- Regularity demands that the model subspace V0 be generated as the linear hull (algebraically or even topologically closed) of the integer shifts of one or a finite number of generating functions
 or
or  . Those integer shifts should at least form a frame for the subspace
. Those integer shifts should at least form a frame for the subspace 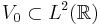 , which imposes certain conditions on the decay at infinity. The generating functions are also known as scaling functions or father wavelets. In most cases one demands of those functions to be piecewise continuous with compact support.
, which imposes certain conditions on the decay at infinity. The generating functions are also known as scaling functions or father wavelets. In most cases one demands of those functions to be piecewise continuous with compact support.
- Completeness demands that those nested subspaces fill the whole space, i.e., their union should be dense in
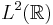 , and that they are not too redundant, i.e., their intersection should only contain the zero element.
, and that they are not too redundant, i.e., their intersection should only contain the zero element.
Important conclusions
In the case of one continuous (or at least with bounded variation) compactly supported scaling function with orthogonal shifts, one may make a number of deductions. The proof of existence of this class of functions is due to Ingrid Daubechies.
There is, because of 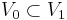 , a finite sequence of coefficients
, a finite sequence of coefficients 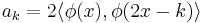 , for
, for 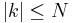 and
and 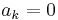 for
for 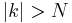 , such that
, such that
Defining another function, known as mother wavelet or just the wavelet
one can see that the space 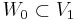 , which is defined as the linear hull of the mother wavelets integer shifts, is the orthogonal complement to
, which is defined as the linear hull of the mother wavelets integer shifts, is the orthogonal complement to 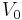 inside
inside 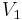 . Or put differently,
. Or put differently, 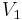 is the orthogonal sum of
is the orthogonal sum of 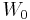 and
and 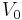 . By self-similarity, there are scaled versions
. By self-similarity, there are scaled versions 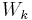 of
of 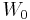 and by completeness one has
and by completeness one has
thus the set
is a countable complete orthonormal wavelet basis in 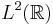 .
.
See also
References
- Chui, Charles K. (1992). An Introduction to Wavelets. San Diego: Academic Press. ISBN 0585470901.
- Akansu, A.N.; Haddad, R.A. (1992). Multiresolution signal decomposition: transforms, subbands, and wavelets. Academic Press. ISBN 978-0-12-047141-6.
- Burrus, C.S.; Gopinath, R.A.; Guo, H. (1997). Introduction to Wavelets and Wavelet Transforms: A Primer. Prentice-Hall. ISBN 0124896009.
- Mallat, S.G. (1999). A Wavelet Tour of Signal Processing. Academic Press. ISBN 012466606X. http://www.cmap.polytechnique.fr/~mallat/book.html.